[ad_1]
Recorrer la historia de las matemáticas lleva a lugares inesperados, en este caso a los campanarios de la Inglaterra del siglo XVII. En aquella época, grupos de campaneros ingleses se reunían regularmente para practicar el arte de tañer campanas. Se propusieron tocar las campanas de un campanario en todos los órdenes posibles sin repetición. Era tal el interés que se escribieron varios tratados al respecto, entre ellos “Tintinnalogia”, de Richard Duckworth y Fabian Stedman. Este problema anticipó una rama de las matemáticas llamada teoría de grupos.
El número de maneras posibles en el que podemos ordenar n campanas viene dado por n! (leído n factorial) y es igual a n!=n.(n-1).(n– 2) …3.2.1. Así, en un campanario con seis campanas, existen 6! = 6.5.4.3.2.1 = 720 maneras distintas de tañerlas; pero no basta con enumerar estos posibles órdenes y tocar uno después de otro, sino que hay que atender a ciertas reglas.
En primer lugar, los campaneros no pueden llevar ‘partituras’ describiendo la secuencia de órdenes. Por tanto, hay que buscar un patrón fácil de recordar, algo que en sí mismo no es demasiado complicado. El problema aparece por las restricciones asociadas a la propia naturaleza de las campanas. Estas son pesadas, van montadas sobre ruedas, y su cadencia es difícil de modificar. En la práctica, esto implica que entre una configuración y la siguiente solo se puede cambiar el orden de las campanas que han tocado seguidas. Por ejemplo, si tenemos cuatro campanas y las llamamos A, B, C, D, la secuencia ACDB indica que tocamos primero la A, después la C, después la D y finalmente la B. Así después de ACDB podemos tañer CADB o ACBD o incluso CABD. Sin embargo, después de ACDB no podemos hacer sonar DCAB. Además, por cuestiones estéticas, se debe empezar y acabar con la misma configuración. Así si se empieza con ABCD, se deben recorrer todas las configuraciones respetando la norma anterior y sin repeticiones, para acabar de nuevo en ABCD.
Es posible, y no muy complicado, encontrar un patrón que cumpla las reglas anteriores de forma recursiva. Es decir, conociendo un patrón para un cierto número de campanas, se puede diseñar un patrón para tocar una campana más. Se han propuesto varias soluciones de este estilo a lo largo de la historia. Por ejemplo, el informático Donald Knuth, en su célebre Art of Computing, cita un algoritmo de Peter Mundy de 1653 que permite hacerlo.
La última condición sobre los patrones tiene que ver con la sonoridad. La moda del siglo XVII imponía que una campana no podía tocarse en la misma posición tres veces seguidas. ¡Ahora sí tenemos un reto! Stedman encontró una solución para este problema con cinco campanas, que está recogida en su “Tintinnalogia”. Su patrón, conocido como Stedman’s doubles, está íntimamente relacionado con la forma en la que el grupo de isometrías del pentágono regular aparece como subgrupo del grupo de permutaciones de las campanas. Si no entiendes de lo que estamos hablando, no te preocupes, Stedman tampoco lo entendería. Estos son conceptos de una rama de las matemáticas que no se formalizó hasta dos siglos después, la Teoría de Grupos.
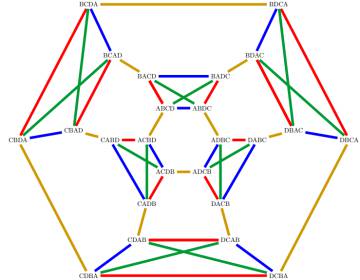
El arte de tañer campanas mantiene sus adeptos en Inglaterra. En 1963, ocho campaneros ingleses tocaron en la Loughborough Bell Foundry ocho campanas en todos los órdenes posibles y sin repetición (un total de 40320 configuraciones distintas). Para ello emplearon 17 horas y 58 minutos. La búsqueda de distintos patrones musicales también continúa. Actualmente se plantea desde una perspectiva que conecta la teoría de grupos y la teoría de grafos. Concretamente, la secuencia en la que se tocan los distintos órdenes de las campanas se corresponde con un camino en un cierto grafo (el grafo de Cayley asociado al grupo de permutaciones) y las restricciones que se imponen al patrón equivalen a propiedades del camino buscado. Este enfoque ya apareció en un trabajo de Robert A. Rankin de 1948, en el que resolvía un problema sobre campanas de 1741, y pervive en trabajos actuales como este o este.
Yago Antolín es Ayudante Doctor en la Universidad Autónoma de Madrid y miembro del ICMAT.
Carolina Vallejo es investigadora Juan de la Cierva en la Universidad Autónoma de Madrid y miembro del ICMAT.
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: «Un matemático es una máquina que transforma café en teoremas».
Edición y coordinación: Ágata Timón (ICMAT).
Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aquí a nuestra newsletter
[ad_2]
Source link
























